[kaka18]

hallo,

also ich komm bei einer aufgabe nicht ganz weiter.

die aufgabe ist, folgende:

man übergibt einer methode ein array aus zahlen (das array hat mind. 3 elemente).

wie überprüft man jetzt, ob die zu übergebende zahlenreihe ein ausschnitt aus der "ORIGINAL" fibonacci reihe ist???


also beispiel:
"Original" fibonacci reihe: 0,1,1,2,3,5,8.....

array: 3,5,8 => true
array: 10,20,30 => false! obwohl es die fibonacci eigenschaft erfüllt

also es reicht nicht aus, nur zu prüfen, ob f(n) = f(n-1) + f(n-2) erfüllt ist.


hoffe habs verständlich genug geschildert^^
kann mir da jemand helfen?

[Robar666]

Um zu prüfen ob es die "Original" Fibonacci Reihe ist würde ich schauen ob das 1.Element 0 und das 2. Element 1 ist, danach kannst du ja jedes Element mit f(n) = f(n-1) + f(n-2) prüfen.

EDIT
Aso leider erst jetzt gesehen, das man auf einen AUSSCHNITT der Original Reihe prüfen soll. Naja dann würde ich zuerst schauen ob die erste Zahl Teil der Original Fibnoacci-Reihe ist und danach prüfen ob das übergebene Array die Fibnoacci Eigenschaften erfüllt (f(n) = f(n-1) + f(n-2)).


EDIT 2
Bevor die Frage auftaucht wie du weißt ob eine Zahl Teil der Original Fibnoacci-Reihe ist, hier zwei Lösungsvorschläge:

1.

Die Original-Reihe solang generieren bis man bei der gesuchten Zahl angelangt ist oder sie überschritten hat.
-> Langsam

2.

Mit dieser Formel: [ Link nur für registrierte Mitglieder sichtbar. Bitte einloggen oder neu registrieren ] rausfinden ob eine Zahl Teil der Fibonacci-Reihe ist:

private static boolean isFibByFormula(long num) {
    double power = (double)num * (double)num;
    double first = 5 * power + 4;
    double second = 5 * power - 4;

    return isWholeNumber(Math.sqrt(first)) || isWholeNumber(Math.sqrt(second));
}

(Geklaut von: [ Link nur für registrierte Mitglieder sichtbar. Bitte einloggen oder neu registrieren ])

[spartan-b292]

Du könntest zum Beispiel die n-te Fibonaccizahl berechnen



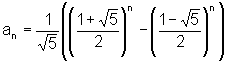
Ist die Zahl kleiner berechnest du die nächste, ist diese Größer ist es keine Fibonacci Zahl, folglich können die anderen auch keine Fibonaccizahlen sein.

Das sollte recht gut gehen, solange die Zahlen nicht zu groß sind.

[Gun_der]

Müssen es denn aufeinanderfolgende Fibonaccizahlen sein?
Das musst du, je nachdem wie die Aufgabe gestellt ist, auch noch beachten.

BSP: [1,3,8] --> true
[0,1,1] --> true

[kaka18]

Müssen es denn aufeinanderfolgende Fibonaccizahlen sein?

ja muss es... es handelt sich um ein ausschnitt aus der fibonacci reihe, also denke ich sollen die zahlen aufeinanderflgen


@ alle anderen

danke erstmal für die antworten.

ich schau mal was ich damit anfangen kann^^

[michederoide]

@Robar666:

Bzgl. deines 1. Punktes: Für große Zahlen stimme ich dir zu. Wenn es aber grundsätzlich um eine Lösung geht, ist es natürlich am einfachsten zu implementieren, wenn man die Fibonacci-Folge bis zur größten der gegebenen Zahlen in ein Array speichert und dann überprüft, ob die gegebenen Zahlen ein "Teilarray" des errechneten Fibonacci-Arrays sind.

Gehen wir mal davon aus, dass das Programm nicht beendet wird, bevor weitere Folgen berechnet werden. Dann könnte man zur Laufzeit dasselbe Array mehrmals verwenden und notfalls erweitern, sobald noch größere Zahlen ankommen.

Man könnte das Programm dann sogar noch theoretisch so erweitern, dass es im Hintergrund (im separaten Thread) die Fibonacci-Folge "unendlich weit vorberechnet" und vor Beendigung das Ergebnis in einer Textdatei speichert.

Dann sieht die Performance wieder etwas besser aus, also bei jedem Start etwas besser (solange es dann nicht länger dauert, die Datei zu lesen, als die nächsten Zahlen zu berechnen).

Eine weitere Idee: Man könnte bestimmte, bereits abgefragte Folgen ebenfalls abspeichern und müsste so, wenn man die gleiche Folge zweimal abfrägt, nur in der Liste nachsehen, ob dort 'true' oder 'false' eingetragen ist.


Die ganzen Ideen sind jetzt vielleicht nicht so übersichtlich dargestellt. Ich habe einfach mal meinen Gedankenfluss textuell hier verewigt (und ich glaube, das kleine Programm schreib ich sogar gleich mal ^^).

LG
michederoide

[ProgMaster]

@michederoide:

Das wäre die programmiertechnisch schlechteste Lösung, die ich mir denken könnte.
1. Speicherverschwendung
2. Das Ermitteln des "Teilarrays" ist ebenso performance-schwach.
3. Jeder neue Programmstart wird länger dauern als der vorherige
4. Das Auslesen der Textdatei, Parsen der Zahlen ist absolut kein Zeitgewinn

Die sinnvollste Lösung wäre nach spartan-b292, die Formel von Moivre-Binet einsetzen und eine "binäre Suche" mittels Näherungsformel.

[michederoide]

1. Speicherverschwendung ist heutzutage nicht mehr das Problem (jeder PC sollte die paar 100 KB Festplattenplatz noch übrig haben; Nach 1000 Zahlen benötigt man nicht mal 10 MB; Wenn du soviel Platz nicht hast, kannst du eine Java-Implementierung schon durch die Größe des JREs/JDKs vergessen).

2. Das Ermitteln eines Teilarrays ist performance-schwächer, als Berechnungen der Form f(n) = f(n - 2) + f(n - 1)?

3. Die Programmstarts werden länger dauern, wenn man die Textdatei wieder einliest, richtig, man könnte aber auch erst dann die Textdatei lesen, wenn notwendig (also z.B. die bereits eingelesenen Werte im Array nicht ausreichen).

4. Wenn die Zahlen "nur" mit Leerzeichen getrennt sind, sind Berechnungen der Form f(n) = f(n - 2) + f(n - 2) normalerweise ab einer gewissen Anzahl performance-schwächer als das Auslesen einer 5 Megabyte-Datei (Größe nur als Beispiel).

LG
michederoide

P.S.: Bei 1 Million Durchgängen �* den ersten 75 Zahlen komme ich darauf, das eine in eine Datei zwischengespeicherte (obwohl diese nicht optimierter Aufruf) Folge insgesamt 884.438.000 Nanosekunden schneller ist als eine reine Berechnung. Also ca. 884 ms. Meine Implementierung IST schneller, wenn oft gerechnet wird (wenn auch nicht viel :P)